Gammakorrektur [Fotolexikon]
Die Gammakorrektur verändert die Helligkeitsinformation von Bildpunkten exponentiell nach der Funktion y = x1/γ. y ist die umgerechnete prozentuale Helligkeit, x die prozentuale Helligkeit vor der Umrechnung und der griechische Buchstabe γ (Gamma) – der Exponent (Hochzahl) – ist eine Konstante (unveränderliche Zahl), die Gammawert genannt wird. Die Gammakorrektur ist notwendig, damit Bilder auf einem Monitor in der richtigen Helligkeit erscheinen.
Computermonitore erzeugen auf dem Schirm eine Intensität nach der Funktion y = xγ. Sie haben ein Gamma um 2,5. Werden sie mit halber Energie (x) angesteuert, um einen Bildpunkt mit halber Intensität abzubilden, leuchten sie nicht mit halber Intensität, sondern geringer (y). Bei Bildpunkten, deren Helligkeit mit 8 Bit kodiert ist (Wertebereich: 0 bis 255), bedeuten der Helligkeitswert 0 Schwarz, 255 Weiß und Werte dazwischen Grau, das umso dunkler ist, je kleiner die Zahl. Die halbe Intensität ist der Zahlenwert 255/2 = 127. Wird dem Monitor (genauer: der Grafikkarte) 127 geschickt (halbe Intensität), ist bei einem Gamma von 2,2 die Intensität auf dem Schirm rund 1/5 und nicht die Hälfte: 0,52,2 ≈ 0,2 = 1/5.
Wird der Input gammakorrigiert, ist der Output auf dem Bildschirm wie gewünscht, da y = (xy)1/y = xy*1/y = x1 = x. Folgende Abbildung zeigt das.
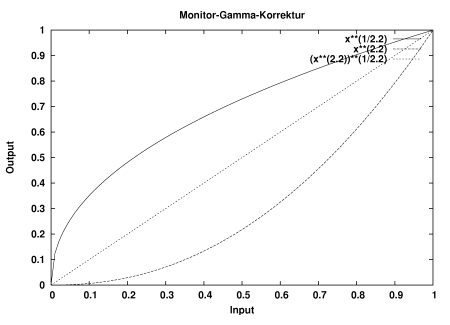
Abbildung: Gammakorrektur des Inputs. Ein Monitor mit Gamma 2,2 erzeugt in Bezug auf den Input exponentiell Intensitäten (Output), die geringer sind als der prozentuale Input (untere Kurve). Werden die Inputs gammakorrigiert (obere Kurve) ist das Ergebnis ein linearer Output (Gerade).
Will ich einen Bildpunkt gammakorrigieren, muss ich wissen, welche Helligkeit er repräsentiert bezogen auf die Maximalhelligkeit. Dazu teile ich seinen Wert durch den Maximalwert (der Maximalwert erzeugt den maximalen Input). Bei 8 Bit-Kodierung ist der Maximalwert 255. Ein Bildpunkt mit dem Helligkeitswert 25 repräsentiert die prozentuale Helligkeit von 25/255 = 0,1. Mit Gammakorrektur: 0,11/2,2 ≈ 0,35. 35 % Input liefert ein Punkt mit 255 * 0,35 ≈ 89. Statt 25 wird die Helligkeitsinformation 89 eingegeben (Gammakorrektur). Kurz: Für 8-Bit-Daten erhalte ich den gammakorrigierten Zahlenwert mit 255 * (x/255)1/γ oder ausgeklammert mit x1/γ * 255/2551/γ. Die folgende Abbildung zeigt zwei Graustufen-Keile mit um jeweils 10 % zunehmender Intensität — einmal linear (oben) und einmal (unten) gammakorrigiert.

Abbildung: Gammakorrektur von Graustufen. Die Intensitäts-Abstufungen sind 10 % bei beiden Graustufenverläufen, oben linear, unten mit Gammakorrektur, Gamma = 2,2. Der Wert 0,1 (10 %) wurde oben berechnet mit 255 (= 100 % = 1, reines Weiß) × 0,1 = 25 und unten mit 255 × 0,11/2,2 = 89. Der lineare Input 127 oberhalb 0,5 (50 % = 0,5; 0,5 * 255 ≈ 127), erzeugt ein dunkleres Grau als die Hälfte der maximalen Helligkeit. Der gammakorrigierte Input 186 (255 * (127/255)1/2,2 ≈ 186) erzeugt die richtige Intensität.
Was geschieht, wenn ein Bild, erstellt mit einem Monitorgamma von 1,8 – üblich bei Macintosh-Rechnern – auf einem Monitor mit Gamma 2,2 – üblich bei Windows – betrachtet wird und umgekehrt? Folgende Abbildung verdeutlicht das:

Abbildung: Gammakorrektur auf verschiedenen Monitoren. Die Erklärung steht im Text unten.
Bilder, erstellt auf dem Macintosh, kodiert mit einem Gamma von 1,8, erscheinen auf einem Windows-Monitor mit Gamma 2,2 dunkler, die Kurve verläuft unterhalb der linearen Darstellung (45°-Gerade). Auf einem Windowsrechner gammakorrigierte Bilder (Gamma 2,2) erscheinen auf dem Macintosh-Monitor (Gamma 1,8) zu hell, die Kurve liegt oberhalb der linearen Darstellung.


Abbildung: Gammakorrektur, Bildbeispiel. Beide Bilder wurden aus einer RAW-Datei konvertiert, das erste mit Gammakorrektur, das zweite ohne. Das Bild ohne Gammakorrektur ist dunkler.
, 03.08.2005.